1 / 112
Three ants are sitting at the three corners of an equilateral triangle. Each ant starts randomly picks a direction and starts to move along the edge of the triangle. What is the probability that none of the ants collide?
2 / 112
How many steps are required to break an m x n bar of chocolate into 1 x 1 pieces? We may break an existing piece of chocolate horizontally or vertically. Stacking of two or more pieces is not allowed.

No Best Answer on this question yet!
Not Yet Asked in Any of the Companies
3 / 112
There are 100 doors, all closed. In a nearby cage are 100 monkeys.
The first monkey is let out and runs along the doors opening every one. The second monkey is then let out and runs along the doors closing the 2nd, 4th, 6th,... all the even-numbered doors. The third monkey is let out. He attends only to the 3rd, 6th, 9th,... doors (every third door, in other words), closing any that is open and opening any that is closed, and so on. After all 100 monkeys have done their work in this way, what state are the doors in after the last pass, which doors are left open and which are closed?
No Best Answer on this question yet!
Asked In : Cavium Networks
4 / 112
There are n students in a class, each in possession of a different personality attribute. As they are new in the school, so they want to know about each other. To help the students, the teacher decides to conduct an activity. The rule for the activity is that the students will share the personality attributes of each other through a series of bilateral conversations (e.g., via a telephone). Assume that in every conversation both parties exchange all the personality attributes they know at the time. What is the minimum number of conversations they need to guarantee that everyone of them gets all the personality attributes?
No Best Answer on this question yet!
Not Yet Asked in Any of the Companies
5 / 112
There are two gates. One goes to hell and the other goes to heaven. The gatekeeper asks a puzzle to Sahil in order to decide which gate he should open for him. Obviously if Sahil answers the puzzle correct , the gate to heaven will be opened else the gate to hell. According to the problem Sahil is given n consecutive integers from 1 to n ,which are written in a row. He has to put signs "+" and "-" in front of them so that the expression obtained is equal to 0 or, if the task is impossible to do,then Sahil should tell the gatekeeper “No solution exists for the given problem “.The gatekeeper expects Sahil to find his answer in minimum time using an efficient approach rather than examining all possible ways to place the signs. Sahil comes to you considering you as his friend. Would you help him out to get to the solution ?
No Best Answer on this question yet!
Asked In : Sapient
6 / 112
There are n glasses on the table, all standing upside down. In one move, you are allowed to turn over exactly n 1 of them. Determine all values of n for which all the glasses can be turned up in the minimum number of moves.
No Best Answer on this question yet!
Asked In : Sapient
7 / 112
Four people need to cross a rickety bridge at night. Unfortunately, they have only one torch and the bridge is too dangerous to cross without one. The bridge is only strong enough to support two people at a time. Not all people take the same time to cross the bridge. Times for each person: 1 min, 2 mins, 7 mins and 10 mins. What is the shortest time needed for all four of them to cross the bridge?
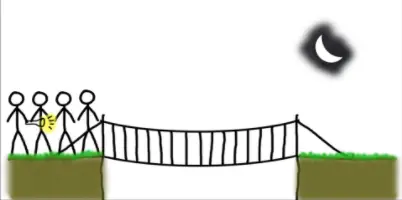
No Best Answer on this question yet!
Asked In : Sapient
8 / 112
A man has two ropes of varying thickness (Those two ropes are not identical, they aren’t the same density nor the same length nor the same width). Each rope burns in 60 minutes. He actually wants to measure 45 mins. How can he measure 45 mins using only these two ropes.
He can't cut the one rope in half because the ropes are non-homogeneous and he can’t be sure how long it will burn.
No Best Answer on this question yet!
Asked In : Sapient
9 / 112
You are standing before two doors. One of the paths leads to heaven and the other one leads to hell. There are two guardians, one by each door. You know one of them always tells the truth and the other always lies, but you don’t know who is the honest one and who is the liar.
You can only ask one question to one of them in order to find the way to heaven. What is the question?
No Best Answer on this question yet!
Asked In : Infosys
10 / 112
You are blindfolded and 10 coins are place in front of you on table. You are allowed to touch the coins, but can’t tell which way up they are by feel. You are told that there are 5 coins head up, and 5 coins tails up but not which ones are which. How do you make two piles of coins each with the same number of heads up? You can flip the coins any number of times.
No Best Answer on this question yet!
Not Yet Asked in Any of the Companies
Puzzle test enable the companies to check the Logical skills of a candidate. Check out these Puzzle topics with answers for the interview! You can choose a topic and speak up your mind through a Gmail type editor.