1 / 10
You are standing before two doors. One of the paths leads to heaven and the other one leads to hell. There are two guardians, one by each door. You know one of them always tells the truth and the other always lies, but you don’t know who is the honest one and who is the liar.
You can only ask one question to one of them in order to find the way to heaven. What is the question?
2 / 10
The Monty Hall Puzzle
You are the contestant on a Game Show. There are 3 doors say A,B and C and behind one door is the prize of a million dollars. The prize is randomly placed and the probability of finding the prize behind any door is 1/3.
You get to pick one door and if you've picked the right door, you win the prize.
There's a catch. After you've chosen a door, the game show host will not immediately open that particular door. The host will open another door that you did not pick and which he knows does not contain the prize. Suppose you had picked door A, and the prize is behind door B, the host will open door C and let you know that there is nothing being door C.
At this point, you will be given a choice: Do you want to stick with your original choice (door A in the example above) or do you want to choose the other unopened door (door B in this example)?
Would you switch your choice?
3 / 10
2 Eggs 100 floor Puzzle
There is a building of 100 floors If an egg drops from the Nth floor or above it will break. If it’s dropped from any floor below, it will not break. You’re given 2 eggs. Find N, while minimizing the number of drops for the worst case?
4 / 10
Red and Blue Marbles Puzzle
There are 2 identical empty jars alongside the jars there were 50 red & 50 blue marbles kept. You need to put all the marbles into both of the jars in such a way that when any jar is selected at random the probability of picking up a red marble is the highest.
5 / 10
There are n coins in a line. (Assume n is even). Two players take turns to take a coin from one of the ends of the line until there are no more coins left. The player with the larger amount of money wins.
6 / 10
There is a circular field of radius 40cm. Around the circular field, there is a walkway of width 4cm. There is a beehive at a distance of 100cm from the center of the circular field. You are standing at the centre of the circle and suddenly the bee's scattering in all the directions and amongst all bee's there is a bee which can be specifically distinguished which comes inside the circular field (at t=0) in and then moves at the constant rate of 10cm/s in a path like this:
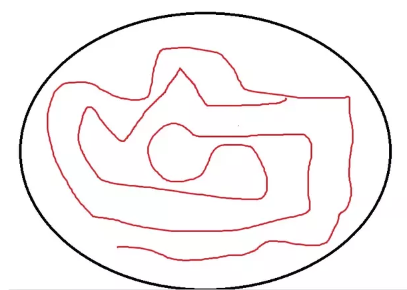
Black boundary represents the circular field and the red path represents the trajectory of the bee.
Estimate the distance covered by the bee after 2 mins.
7 / 10
If 5/2 artists make 5/2 paintings using 5/2 canvases in 5/2 days then how many artists r required to make 25 paintings using 25 canvases in 25 days?
8 / 10
A man is on an island, he doesn't know swimming, deep water is around the island and in water there are sharks & Crocodiles so if he goes in water they will eat him, there is fire broked in island he has to save himself, he is in east end and air is flowing from west to east direction and fire will reach east end within half-an-hour. How will he save himself?
9 / 10
Monkey and Coconut Problem
5 person crash-landed on a beach. they collected few coconuts in a pile. as it was getting dark, they decide to divide it equally next morning. one person will take care of the coconuts. 1st person decided to divide the coconuts into equal parts and decided to hide his part. he then mixed the remaining coconuts into a pile but forgot 1 coconut, so he gave it to the monkey. next day, 2nd person also did the same.i.e. divided into equal parts, hid his part and gave 1 coconut to the monkey. what will be the minimum quantity of coconuts in the pile?
10 / 10
Pirates of the Caribbean
Five pirates discover a chest full of 100 gold coins. The pirates are ranked by their ages. Pirate 5 is 50 years old, Pirate 4 is 49, and so on down to Pirate 1. To divide up the loot, they agree on the following:
The most senior pirate will propose a distribution of the booty. All pirates will then vote, including the most senior pirate, and if at least 50% of the pirates on board accept the proposal, the gold is divided as proposed. If not, the most senior pirate is murdered. Then the process starts over with the next most senior pirate until a plan is approved.
All Pirates are equally intelligent and selfish. Their preference is first to remain alive, and next to get as much gold as possible and finally, if given a choice between otherwise equal outcomes, to have fewer pirates on the boat.
Assume you are the senior most pirate in the group. Come up with a plan that maximizes your gold, and others will accept. How will you divide the coins?
Infosys Practice Set

