TCS online aptitude test questions answers

Answer: Option E

We can fix A and B in two ways with 7 letters in between them. Now 7 letters can be selected and arranged in between A and B in 24P7 ways. Now Consider these 9 letters as a string. So now we have 26 - 9 + 1 = 18 letters
These 18 letters are arranged in 18! ways.
So Answer is 2 x 24P7 x 18!
OR 2 x 24P7 x 18! = 36 x 24!.

Answer: Option D

Let the age of Usha is 3x then Nisha is x and Asha is 25
Also Usha 34, Nisha y, and Asha 2y.
We know that 3x - 34 = x - 2y = 25 - 2y
Solving above three equations we get x = 9, y = 16
Their ages are 34, 16, 32. whose sum = 82. So after 18 years their ages will be equal to 100. So Usha age is 34 + 6 = 40

Answer: Option A

52+50+78 = 180

182

Answer: Option B

Maximum power of 5 in the above expression can be calculated like this. Count all the powers of 5 in the above expression. So number of zeroes are 9.

Answer: Option B

A leap year has 366 day which is 52 full weeks + 2 odd days. Now these two odd days may be (sun + mon), (mon + tue), .... (Sat + sun). Now there are total 7 ways. Of which Sunday appeared two times. So answer 2/7

Answer: Option B

Total ways to move from A to the junction: There are 13 upward ways, 3 right side ways this Ant can move. Now these 16 ways may be in any order. So number of ways of arrangements = 16!/(13! * 3!) = 560
Similarly, from the junction to F, Total 12 upward ways and 5 right-side ways. These 17 ways can be in any order. So Total ways = 17!/(12! * 5!) = 6188.
Total ways to move from A to F = 560 * 6188 = 3465280

Answer: Option C

Let us assume we need "a" liters of 13% acid solution and "b" liters of 43% acid solution. Now
=>18 = (a * 13 + b * 43)/(a + b)
=>a/b = 5/1
So we need 100 liters of 13% acid solution, and 20 liters of 18% acid solution.
Final cost = 82 * 67 + 66 * 33 = 7672

Answer: Option C

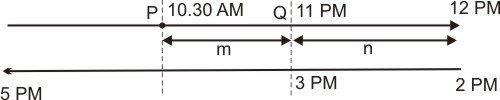
Vehicle A overtaken B at 10.30 am and reached X at 12 pm.  It started at 2 pm and met B at 3 pm at Q. It means, Vehicle A took one hour to cover distance 'n', So it should be at Q at 11 pm.  It is clear that Vehicle A takes 0.5 hour to cover distance 'm'. 

Now vehicle B travelled from 10.30 am to 3 pm to meet A. So it took 4.5 hours to cover m.  So Speeds ratio = 4.5 : 0.5 = 9 : 1.

Now Vehicle A took a total of 1.5 + 3 = 4.5 hours to travel fro P to Y. So It must take 4.5 * 9 + 1 = 41.5 hours

Answer: Option A

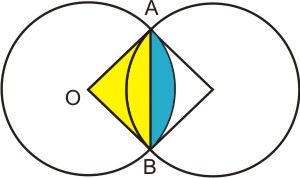
 We have to find the area of the blue shaded one and double it to get the area common to the both.

Now this can be calculated as Area of the sector OAB - Area of the Triangle OAB.

As OA and OB are perpendicular, area of the sector OAB = 90/360 π (1)^2 = π/4

Area of the triangle OAB = 1/2 * 1 * 1 = 1/2

Area common to both = (π/4 - 1/2)/2 = π/2 - 1

Answer: Option C

As the final average is 105/4, initial number of pages should be 2 more than a four multiple. So in the given options, we will check option C.
Total = n(n+1)/2=(50 * 51)/2 = 1275
Final total = 48 * 105/4 = 1260
So sum of the pages = 15. The page numbers are 7, 8